Types of Transforms

QuickDraw 3D supports a number of different ways of transforming geometric objects. Equivalently, these transforms are ways of transforming coordinate systems containing geometric objects.

Matrix Transforms

A matrix transform is any transform specified by an affine, invertible 4-by-4 matrix. QuickDraw 3D does not check that the matrix you specify is affine or invertible, so it is your responsibility to ensure that the matrix has these qualities.

A matrix transform is the most general type of transform and can be used to represent any of the other kinds of transforms. If, however, you just want to apply a translation to an object, it's better to use a translate transform instead of a matrix transform. By using the more specific type of transform object, you allow renderers and shaders to apply optimizations that might not apply to a more general transform.

Translate Transforms

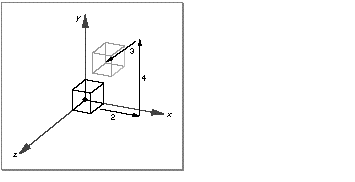
A translate transform translates an object along the x , y , and z axes by specified values. You specify the desired translation values using a vector. For example, to translate an object by 2 units along the positive x axis, by 4 units along the positive y axis, and by 3 units along the positive z axis, you could define a vector like this:



 
TQ3Vector3D                     myVector;

TQ3TransformObject              myTransform;



Q3Vector3D_Set(&myVector, 2.0, 4.0, 3.0);

myTransform = Q3TranslateTransform_New(&myVector);

Figure 7 shows a unit cube before and after a translate transform is applied.

Figure 7 A translate transform

Scale Transforms

A scale transform scales an object along the x , y , and z axes by specified values. Figure 8 shows a unit cube before and after applying a scale transform.

Figure 8 A scale transform

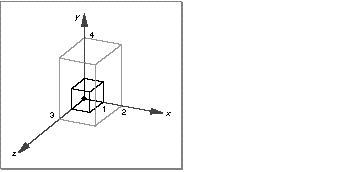
As with a translate transform, you specify the desired scale transform by using a vector. For example, to scale an object by a factor of 2 along the positive x axis, by a factor of 4 along the positive y axis, and by a factor of 3 along the positive z axis, you could define a vector like this:



 
TQ3Vector3D             myVector;



Q3Vector3D_Set(&myVector, 2.0, 4.0, 3.0);

Rotate Transforms

A rotate transform rotates an object about the x , y , or z axis by a specified number of radians at the origin.

To specify a rotate transform, you fill in the fields of a rotate transform data structure, which specifies the axis of rotation and the number of radians to rotate. You can use QuickDraw 3D macros to convert degrees to radians, if you prefer to work with degrees. (See the chapter "Mathematical Utilities" for details.) Figure 9 shows a unit cube before and after applying a rotate transform.

Figure 9 A rotate transform

Rotate-About-Point Transforms

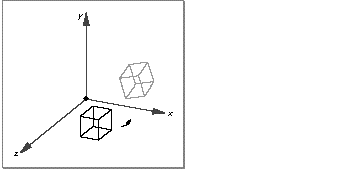
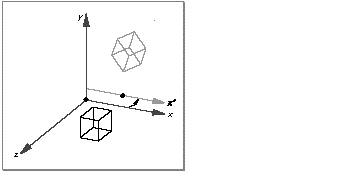
A rotate-about-point transform rotates an object about the x , y , or z axis by a specified number of radians at an arbitrary point in space. To specify a rotate-about-point transform, you fill in the fields of a rotate-about-point transform data structure, which specifies the axis of rotation, the point of rotation, and the number of radians to rotate. Figure 10 shows a unit cube before and after applying a rotate-about-point transform.

Figure 10 A rotate-about-point transform

Rotate-About-Axis Transforms

A rotate-about-axis transform rotates an object about an arbitrary axis in space by a specified number of radians at an arbitrary point in space. To specify a rotate-about-axis transform, you fill in the fields of a rotate-about-axis transform data structure, which specifies the axis of rotation, the point of rotation, and the number of radians to rotate. Figure 11 shows a unit cube before and after applying a rotate-about-axis transform.

Figure 11 A rotate-about-axis transform

The Reset Transform

When transforms are submitted to a view, either directly through an immediate-mode call such as Q3ScaleTransform_Submit or a retained-mode call such as Q3Transform_Submit , or indirectly by inclusion in a group, the view's current transformation matrix is concatenated with the submitted matrix to form the new current transformation matrix.

An application can take advantage of this transformation stacking behavior in hierarchical modelling; the view can maintain a stack of transformations that the application may push and pop. The application can do this explicitly, using Q3View_Push and Q3View_Pop , or implicitly by using groups, which push and pop transformations when they are entered and exited. In a push, the current transformation is pushed onto a stack, but a copy remains as the current transfomation. Subsequent transformation submissions concatenate their matrices with the current transformation.

However, this behavior is not always desirable. Suppose an application traverses a hierarchy, either in mixed or immediate mode, using sequences of push-transform-polygon-pop actions. If the application wants to draw a shape untransformed in the middle of such a sequence, (because, for example, the shape is already drawn in world space coordinates), then the application would have to get the current transformation, invert it, and submit the inverted transformation, thereby resolving the current transformation in the view to the identity matrix. Such a sequence of actions would usually be bracketed by a push-pop sequence. Because obtaining the current matrix, inverting it, and submitting the inverted matrix require significant amounts of processing time, and because inversion cannot be perfectly precise (because of floating-point approximations), QuickDraw 3D includes a reset transform. It resets the current transformation to identity (that is, equivalent to the 4x4 identity matrix).

The routines that implement the reset transform are described in "Creating and Submitting the Reset Transform" .